Předpětí svorek bipolárního tranzistoru pomocí vypočítané sítě odporového děliče pro zajištění optimálního výkonu a odezvy spínání se nazývá předpětí děliče napětí.
V předchozí návrhy zkreslení že jsme se naučili zkreslený proud I CQ a napětí V CEQ byly funkcí aktuálního zisku (β) BJT.
Jelikož však víme, že β může být citlivý na změny teploty, zejména u křemíkových tranzistorů, a také skutečná hodnota beta není často správně identifikována, mohlo by být vhodné vyvinout v obvodu BJT zkreslení napětí-dělič, které může být menší náchylný k teplotám, nebo jednoduše nezávislý na samotné BJT beta verzi.

Uspořádání předpětí děliče napětí na obr. 4.25 lze považovat za jeden z těchto návrhů.
Při vyšetření s přesný základ náchylnost k odchylkám v beta verzi vypadá opravdu skromně. Pokud jsou proměnné obvodu správně zpracovány, úrovně I CQ a V CEQ může být prakticky úplně nezávislá na beta verzi.
Pamatujte si z dřívějších vysvětlení, že Q-bod je charakterizován pevnou úrovní ICQ a VCEQ, jak je ukázáno na obr. 4.26.
Stupeň I BQ se může měnit v závislosti na variaci v beta verzi, ale provozní bod kolem charakteristik identifikovaných I CQ a V CEQ mohou snadno zůstat beze změny, pokud se použijí příslušné pokyny pro zapojení.
Jak bylo uvedeno výše, najdete několik přístupů, které lze použít k prozkoumání nastavení děliče napětí.
Důvod výběru konkrétních jmen pro tento okruh bude zřejmý během naší analýzy a bude o něm pojednáno v budoucích příspěvcích.
Úplně první je přesná technika které lze provést na jakémkoli nastavení děliče napětí.
Druhý se nazývá přibližná metoda, a jeho implementace se stane proveditelnou, když budou splněny určité faktory. The přibližný přístup umožňuje mnohem přímější analýzu s minimálním úsilím a časem.
Navíc to může být velmi užitečné pro „režim návrhu“, o kterém si povíme v dalších částech.
Celkově, protože „přibližný přístup“ lze pracovat s většinou podmínek, a proto musí být hodnoceny se stejnou mírou pozornosti jako „přesná metoda“.
Přesná analýza
Naučme se, jak metoda přesná analýza lze implementovat s následujícím vysvětlením
S odkazem na následující obrázek lze vstupní stranu sítě reprodukovat, jak je znázorněno na obr. 4.27 pro analýzu stejnosměrného proudu.
The Théveninův ekvivalent síť pro návrh na levé straně základny BJT B lze potom určit způsobem, jak je znázorněno níže:

RTh : Vstupní napájecí body jsou nahrazeny ekvivalentním zkratem, jak je znázorněno na obr. 4.28 níže.


ETh: Zdroj napájecího napětí V DC je přivedeno zpět do obvodu a napětí Théveninova obvodu s otevřeným obvodem, jak je uvedeno na obr. 4.29 níže, je hodnoceno takto:
Implementací pravidla děliče napětí jsme dospěli k následující rovnici:


Dále vytvořením designu Thévenin, jak je znázorněno na obr. 4.30, hodnotíme I BQ nejprve uplatněním Kirchhoffova zákonu napětí ve směru hodinových ručiček pro smyčku:
ETh - IBRTh - VBE - IERE = 0
Jak víme IE = (β + 1) B Nahrazením ve výše uvedené smyčce a řešením pro I B dává:

Rovnice. 4.30

Na první pohled můžete cítit ekv. (4.30) vypadá zcela odlišně od ostatních dosud vyvinutých rovnic, ale bližší pohled ukáže, že čitatel je jen rozdílem dvou voltových úrovní, zatímco jmenovatel je výsledkem odporu základny + emitor, což se odráží podle (β + 1) a je bezpochyby velmi podobný ekv. (4,17) ( Smyčka základního vysílače )
Jakmile se IB vypočítá pomocí výše uvedené rovnice, zbytek velikostí v návrhu lze identifikovat stejnou metodou, jakou jsme udělali pro síť emitor-bias, jak je uvedeno níže:

Rovnice (4.31)

Řešení praktického příkladu (4.7)
Vypočítejte stejnosměrné předpětí V TENTO a aktuální I C v níže zobrazené síti děliče napětí Obr. 4.31
Obrázek 4.31 Beta stabilizovaný obvod pro příklad 4.7.

Přibližná analýza
Ve výše uvedené části jsme se naučili „přesnou metodu“, zde probereme „přibližnou metodu“ analýzy děliče napětí obvodu BJT.
Můžeme nakreslit vstupní fázi sítě děliče napětí založené na BJT, jak je znázorněno na obrázku 4.32 níže.
Odpor Ri lze považovat za ekvivalent odporu mezi základní a zemnicí linkou obvodu a RE jako odpor mezi emitorem a zemí.
Z našich předchozích diskusí [Rov. (4.18)] víme, že odpor reprodukovaný nebo odrážený mezi základnou / emitorem BJT je vysvětlen rovnicí Ri = (β + 1) RE.
Pokud vezmeme v úvahu situaci, kdy Ri je podstatně větší než odpor R2, bude mít za následek IB relativně menší než I2 (pamatujte, že proud se vždy snaží najít a přejít na směr minimálního odporu), a tedy I2 se otočí přibližně stejně jako I1.
Vzhledem k tomu, že přibližná hodnota IB je v podstatě nulová ve vztahu k I1 nebo I2, pak I1 = I2 a R1 a R2 lze považovat za prvky řady.

Obrázek 4.32 Obvod částečného zkreslení pro výpočet přibližného základního napětí V B .
Napětí napříč R2, které původně představovalo základní napětí, lze vyhodnotit, jak je znázorněno níže, pomocí sítě pravidel děliče napětí:

Nyní od té doby Ri = (β + 1) RE ≅ b RE, o podmínce, která potvrzuje, zda je provedení metody přiblížení možné nebo ne, rozhoduje rovnice:

Jednoduše řečeno, pokud je hodnota RE krát hodnota β, není menší než 10násobek hodnoty R2, pak může být dovoleno provést přibližnou analýzu s optimální přesností
Po vyhodnocení VB lze velikost VE určit pomocí rovnice:

zatímco proud emitoru lze vypočítat pomocí vzorce:

Napětí z kolektoru do emitoru lze identifikovat pomocí následujícího vzorce:
VCE = VCC - ICRC - IERE
Nicméně od té doby IE ≅ IC, dospějeme k následující rovnici:

Je třeba poznamenat, že v sérii výpočtů, které jsme provedli z rovnice. (4.33) prostřednictvím ekv. (4.37) ,, prvek β nemá nikde žádnou přítomnost a IB nebyl vypočítán.
To znamená, že Q-bod (stanovený I. CQ a V CEQ ) ve výsledku nezávisí na hodnotě β
Praktický příklad (4.8):
Aplikujme analýzu na naše dřívější Obrázek 4.31 pomocí přibližného přístupu a porovnejte řešení pro ICQ a VCEQ.

Zde pozorujeme, že úroveň VB je identická s úrovní ETh, jak je hodnoceno v našem předchozím příkladu 4.7. To v zásadě znamená, že rozdíl mezi přibližnou analýzou a přesnou analýzou je ovlivněn RTh, který je odpovědný za oddělení ETh a VB v přesné analýze.
Kupředu

Další příklad 4.9
Pojďme provést přesnou analýzu z příkladu 4.7, pokud je β sníženo na 70, a zjistíme rozdíl mezi řešeními pro ICQ a VCEQ.

Řešení
Tento příklad nelze brát jako srovnání přesné a přibližné strategie spíše pouze pro testování míry, ve které se může Q-bod pohybovat v případě, že velikost β je snížena o 50%. RTh a ETh jsou uvedeny stejně:
Uspořádání výsledků do tabulky nám dává následující:

Z výše uvedené tabulky můžeme jednoznačně zjistit, že obvod relativně nereaguje na změnu hladin β. Navzdory skutečnosti, že velikost β byla významně snížena o 50%, z hodnoty 140 na 70, ačkoli hodnoty ICQ a VCEQ jsou v zásadě stejné.
Další příklad 4.10
Vyhodnoťte úrovně I CQ a V CEQ pro síť děliče napětí, jak je znázorněno na obr. 4.33, použitím přesný a přibližný přístupy a porovnat výsledná řešení.

V tomto scénáři jsou podmínky uvedené v rovnici (4.33) nemusí být spokojeni, ale odpovědi nám mohou pomoci identifikovat rozdíl v řešení s podmínkami rovnice. (4.33) nebere v úvahu.
Obrázek 4.33 Dělič napětí síť pro příklad 4.10.

Řešení pomocí přesné analýzy:

Řešení pomocí přibližné analýzy:
Z výše uvedených hodnocení jsme schopni vidět rozdíl mezi výsledky dosaženými přesnými a přibližnými metodami.
Výsledky ukazují, že já CQ je přibližně o 30% vyšší pro přibližnou metodu, zatímco V CEQ je o 10% nižší. I když výsledky nejsou zcela identické, vzhledem k tomu, že βRE je jen 3krát větší než R2, výsledky také nejsou ve skutečnosti příliš daleko od sebe.
Řekl jsem, že pro naši budoucí analýzu budeme převážně spoléhat na Eq. (4.33) k zajištění maximální podobnosti mezi dvěma analýzami.
Předchozí: Emitter-Stabilized BJT Bias Circuit Další: Bipolární přechodový tranzistor (BJT) - konstrukční a provozní podrobnosti

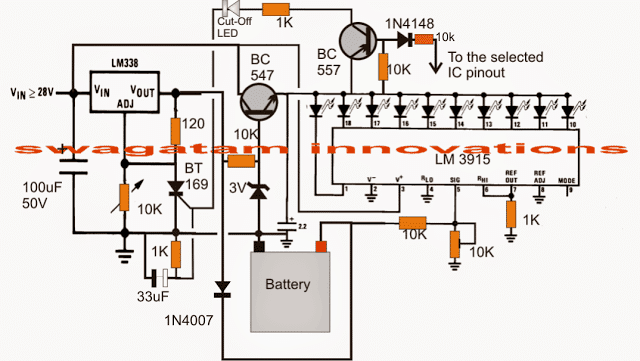
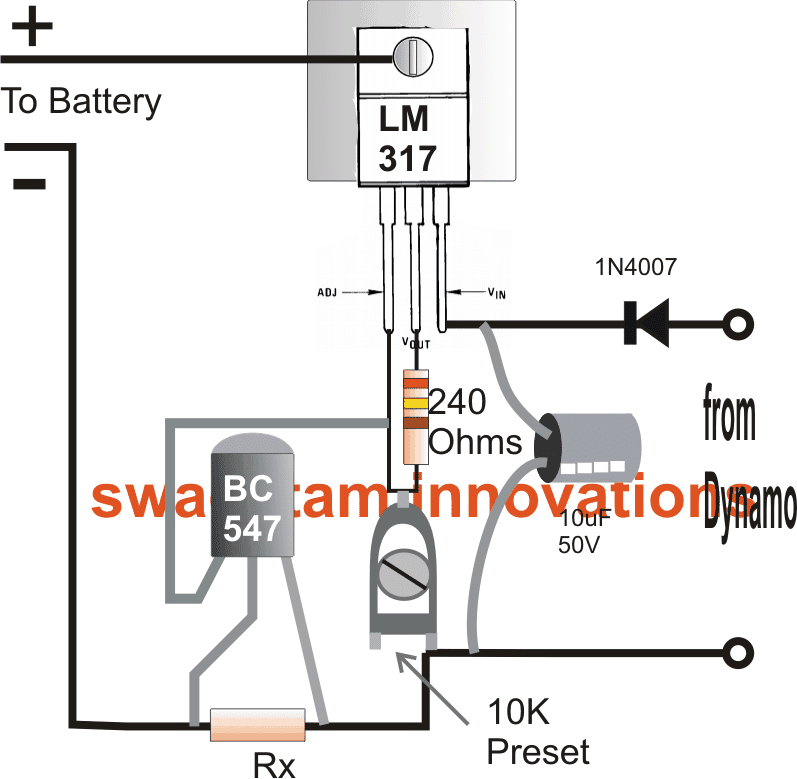
![Obvody nabíječky baterií 12V [využívající tranzistory LM317, LM338, L200]](https://electronics.jf-parede.pt/img/battery-chargers/11/12v-battery-charger-circuits-using-lm317.png)