Podle definice uvedené v Wikipedia elektrický transformátor je stacionární zařízení, které prostřednictvím magnetické indukce vyměňuje elektrickou energii přes několik blízko vinutých cívek.
Neustále se měnící proud v jednom vinutí transformátoru generuje měnící se magnetický tok, který následně indukuje měnící se elektromotorickou sílu na druhou cívku postavenou na stejném jádru.

Základní pracovní princip
Transformátory v zásadě fungují tak, že přenášejí elektrickou energii mezi dvojici cívek prostřednictvím vzájemné indukce, aniž by byly závislé na jakékoli formě přímého kontaktu mezi dvěma vinutími.
Tento proces přenosu elektřiny indukcí poprvé prokázal Faradayův zákon indukce v roce 1831. Podle tohoto zákona je indukované napětí na dvou cívkách vytvářeno v důsledku měnícího se magnetického toku obklopujícího cívku.
Základní funkcí transformátoru je zvýšit nebo snížit střídavé napětí / proud v různých poměrech podle požadavků aplikace. O proporcích rozhoduje počet závitů a poměr otáček vinutí.
Analýza ideálního transformátoru
Můžeme si představit ideální transformátor jako hypotetický design, který může být prakticky bez jakékoli ztráty. Navíc tento ideální design může mít své primární a sekundární vinutí dokonale vzájemně spojené.
Znamená to, že magnetické spojení mezi dvěma vinutími je vedeno jádrem, jehož magnetická permeabilita je nekonečná, a indukčnostmi vinutí při celkové nulové magnetomotorické síle.
Víme, že v transformátoru se aplikovaný střídavý proud v primárním vinutí pokouší vynutit měnící se magnetický tok uvnitř jádra transformátoru, který zahrnuje také sekundární vinutí obklopené kolem něj.
Kvůli tomuto proměnlivému toku je elektromagnetická síla (EMF) indukována na sekundárním vinutí elektromagnetickou indukcí. To má za následek generování toku na sekundárním vinutí s velikostí, která je opačná, ale rovná se toku primárního vinutí, podle Lenz'zův zákon .
Jelikož jádro nese nekonečnou magnetickou permeabilitu, je celý (100%) magnetický tok schopen přenášet se přes dvě vinutí.
To znamená, že když je primární zdroj vystaven zdroji střídavého proudu a zátěž je připojena ke svorkám sekundárního vinutí, protéká proud příslušným vinutím ve směrech, jak je naznačeno v následujícím schématu. V tomto stavu je magnetomotorická síla jádra neutralizována na nulu.

Obrázek s laskavým svolením: https://commons.wikimedia.org/wiki/File:Transformer3d_col3.svg
V této ideální konstrukci transformátoru, protože přenos toku přes primární a sekundární vinutí je 100%, podle Faradayova zákona bude indukované napětí na každém z vinutí dokonale úměrné počtu závitů vinutí, jak je znázorněno v následujícím postava:

Zkušební video Ověření lineárního vztahu mezi primárním / sekundárním poměrem otáčení.
POMĚRY OBRATŮ A NAPĚTÍ
Pokusme se podrobně porozumět výpočtům poměru otáček:
Čistá velikost napětí indukovaného z primárního na sekundární vinutí je jednoduše určena poměrem počtu závitů navinutých na primární a sekundární sekci.
Toto pravidlo však platí pouze v případě, že je transformátor blízký ideálnímu transformátoru.
Ideálním transformátorem je transformátor, který má zanedbatelné ztráty ve formě efektu kůže nebo vířivého proudu.
Vezměme si příklad na obrázku 1 níže (pro ideální transformátor).
Předpokládejme, že primární vinutí se skládá z přibližně 10 závitů, zatímco sekundární pouze s jedním vinutím. V důsledku elektromagnetické indukce se linie toku generovaného napříč primárním vinutím v reakci na vstupní střídavé napětí střídavě rozšiřují a zhroutí a protínají 10 otáček primárního vinutí. To má za následek přesně úměrné množství napětí indukovaného přes sekundární vinutí v závislosti na poměru otáček.

Vinutí dodávané se střídavým vstupem se stává primárním vinutím, zatímco doplňkové vinutí, které produkuje výstup magnetickou indukcí z primárního, se stává sekundárním vinutím.
Obrázek 1)
Vzhledem k tomu, že sekundární má pouze jednu otáčku, zažívá úměrný magnetický tok přes její jedinou otáčku vzhledem k 10 otáčkám primární.
Proto, protože napětí aplikované na primární je 12 V, pak by každé z jeho vinutí bylo vystaveno čítači EMF 12/10 = 1,2 V, a to je přesně velikost napětí, které by ovlivňovalo jednu otáčku přítomnou napříč sekundární sekce. Je to proto, že má jediné vinutí, které je schopné extrahovat pouze stejné ekvivalentní množství indukce, které může být k dispozici v jednom otočení přes primární.
Sekundární s jediným otočením by tedy dokázal extrahovat 1,2 V z primárního.
Výše uvedené vysvětlení naznačuje, že počet závitů na primární transformátoru odpovídá lineárně napájecímu napětí na něm a napětí se jednoduše dělí počtem závitů.
Takže ve výše uvedeném případě, protože napětí je 12V a počet závitů je 10, bude čistý čítač EMF indukovaný přes každý z závitů 12/10 = 1,2V
Příklad č. 2
Nyní si představme obrázek 2 níže, který ukazuje podobný typ konfigurace jako na obrázku 1. očekávejte sekundární, která má nyní 1 další tah, tj. 2 počty tahů.

Není nutné říkat, že nyní by sekundární jednotka procházela dvakrát více řádky toku ve srovnání se stavem na obrázku 1, který měl jen jednu zatáčku.
Takže zde by sekundární vinutí mělo číst kolem 12/10 x 2 = 2,4 V, protože tyto dva závity by byly ovlivněny velikostí čítače EMF, která by mohla být ekvivalentní napříč dvěma vinutími na primární straně trafa.
Z výše uvedené diskuse tedy obecně můžeme usoudit, že v transformátoru je vztah mezi napětím a počtem závitů přes primární a sekundární poměrně lineární a proporcionální.
Čísla otočení transformátoru
Odvozený vzorec pro výpočet počtu závitů libovolného transformátoru lze tedy vyjádřit jako:
Es / Ep = Ns / Np
kde,
- Es = sekundární napětí ,
- Ep = primární napětí,
- Ns = počet sekundárních závitů,
- Np = počet primárních tahů.
Poměr primárního sekundárního obratu
Bylo by zajímavé poznamenat, že výše uvedený vzorec označuje přímý vztah mezi poměrem sekundárního k primárnímu napětí a sekundárním k primárnímu počtu závitů, které jsou označeny jako přiměřené a stejné.
Výše uvedená rovnice může být proto vyjádřena jako:
Ep x Ns = Es x Np
Dále můžeme odvodit výše uvedený vzorec pro řešení Es a Ep, jak je uvedeno níže:
Es = (Ep x Ns) / Np
podobně,
Ep = (Es x Np) / Ns
Výše uvedená rovnice ukazuje, že pokud jsou k dispozici jakékoli 3 velikosti, lze čtvrtou velikost snadno určit řešením vzorce.
Řešení praktických problémů s vinutím transformátoru
Případ v bodě 1: Transformátor má v primární sekci 200 závitů, v sekundárním 50 závitů a přes primární (Ep) připojených 120 voltů. Jaké může být napětí na sekundárním (E)?
Dané:
- Np = 200 otáček
- Ns = 50 otáček
- Ep = 120 voltů
- Je =? volty
Odpovědět:
Es = EpNs / Np
Střídání:
Es = (120 V x 50 otáček) / 200 otáček
Es = 30 voltů
Případ v bodě 2 : Předpokládejme, že máme 400 závitů drátu v cívce se železným jádrem.
Předpokládejme, že jako primární vinutí transformátoru je nutné použít cívku. Vypočítejte počet závitů, které je třeba na cívku navinout, aby se získalo sekundární vinutí transformátoru, aby se zajistilo sekundární napětí jednoho voltu v situaci, kdy primární napětí je 5 voltů?
Dané:
- Np = 400 otáček
- Ep = 5 voltů
- Es = 1 volt
- Ns =? zatáčky
Odpovědět:
EpNs = EsNp
Transpozice pro Ns:
Ns = EsNp / Ep
Střídání:
Ns = (1 V x 400 otáček) / 5 voltů
Ns = 80 otáček
Mít na paměti: Poměr napětí (5: 1) je ekvivalentní s poměrem vinutí (400: 80). Příležitostně, jako náhrada za konkrétní hodnoty, zjistíte, že vám je přiřazen poměr otáček nebo napětí.
V případech, jako je tento, můžete jednoduše předpokládat libovolné číslo pro jedno z napětí (nebo vinutí) a vypočítat další alternativní hodnotu z poměru.
Pro ilustraci předpokládejme, že poměr navíjení je přiřazen 6: 1, můžete si představit množství otáček pro primární sekci a zjistit ekvivalentní sekundární počet závitů pomocí podobných poměrů jako 60:10, 36: 6, 30: 5 atd.
Transformátor ve všech výše uvedených příkladech nese menší počet závitů v sekundární sekci ve srovnání s primární sekcí. Z tohoto důvodu můžete najít menší množství napětí na sekundární části trafa než na primární straně.
Co jsou transformátory pro zesílení a zeslabení
Transformátor, který má jmenovité napětí na sekundární straně nižší než jmenovité napětí na primární straně, se označuje jako a KROKOVÝ transformátor .
Nebo alternativně, pokud je střídavý vstup aplikován na vinutí, které má vyšší počet závitů, pak transformátor funguje jako transformátor sestupný.
Poměr sestupného transformátoru čtyři ku jedné je zapsán jako 4: 1. Transformátor, který zahrnuje menší počet závitů na primární straně ve srovnání se sekundární stranou, bude generovat vyšší napětí přes sekundární stranu ve srovnání s napětím připojeným přes primární stranu.
Transformátor, který má sekundární stranu dimenzovanou na vyšší napětí než na primární straně, se označuje jako STEP-UP transformátor. Nebo alternativně, pokud je AC vstup aplikován na vinutí, které má nižší počet závitů, pak transformátor funguje jako zesilovací transformátor.
Poměr zesilovacího transformátoru jedna ku čtyřem musí být zapsán jako 1: 4. Jak můžete vidět ve dvou poměrech, že velikost primárního bočního vinutí je důsledně uvedena na začátku.
Můžeme použít krokový transformátor jako krokový transformátor a naopak?
Ano, určitě! Všechny transformátory pracují se stejným základním principem, jaký je popsán výše. Použití zesilovacího transformátoru jako zesilovacího transformátoru jednoduše znamená přepínání vstupních napětí na jejich primárním / sekundárním vinutí.
Například pokud máte běžný krokový transformátor napájení, který vám poskytuje výstup 12-0-12V ze vstupu 220V střídavého proudu, můžete použít stejný transformátor jako krokový transformátor pro výrobu výstupu 220V z 12V střídavého proudu vstup.
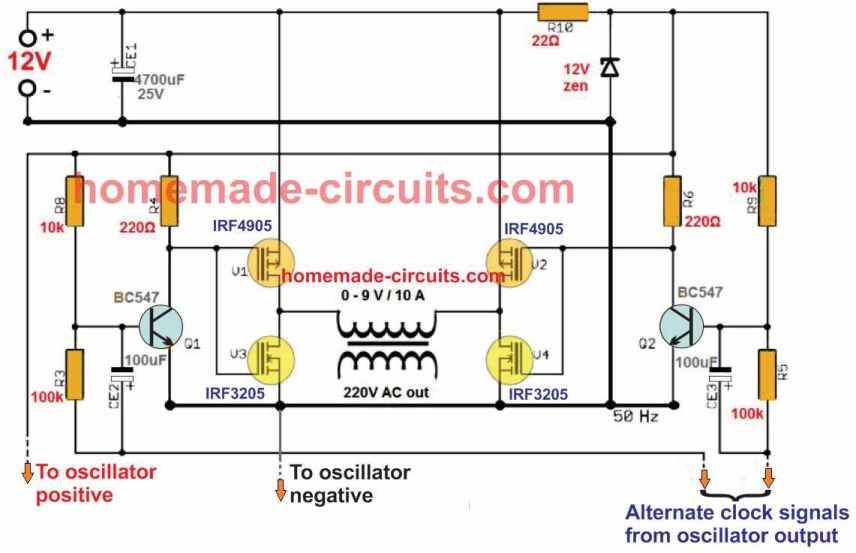
Klasickým příkladem je obvod měniče kde transformátory nemají v sobě nic zvláštního. Všichni pracují s použitím běžných sestupných transformátorů připojených opačným způsobem.
Dopad zatížení
Kdykoli je zátěž nebo elektrické zařízení připojeno přes sekundární vinutí transformátoru, protéká proud a zesilovače přes sekundární stranu vinutí spolu se zátěží.
Magnetický tok generovaný proudem v sekundárním vinutí interaguje s magnetickými linkami toku generovaného zesilovači na primární straně. Tento konflikt mezi dvěma linkami toků je generován jako výsledek sdílené indukčnosti mezi primárním a sekundárním vinutím.
Vzájemný tok
Absolutní tok v materiálu jádra transformátoru převládá jak v primárním, tak v sekundárním vinutí. Je to navíc způsob, kterým je elektrická energie schopna migrovat z primárního vinutí na sekundární vinutí.
Vzhledem k tomu, že tento tok spojuje obě vinutí, jev obecně známý jako MUTUAL FLUX. Také indukčnost, která generuje tento tok, převládá u obou vinutí a nazývá se vzájemná indukčnost.
Obrázek (2) níže ukazuje tok vytvářený proudy v primárním a sekundárním vinutí transformátoru při každém zapnutí napájecího proudu v primárním vinutí.

Obrázek (2)
Kdykoli je odpor zátěže připojen k sekundárnímu vinutí, napětí stimulované do sekundárního vinutí spouští proud, který cirkuluje v sekundárním vinutí.
Tento proud produkuje kroužky toku kolem sekundárního vinutí (označené jako tečkované čáry), které mohou být alternativou k poli toku kolem primárního (Lenzův zákon).
V důsledku toho tok kolem sekundárního vinutí ruší většinu toku kolem primárního vinutí.
S menším množstvím toku obklopujícího primární vinutí se reverzní emf sníží a více zesilovače je nasáváno ze zdroje. Doplňkový proud v primárním vinutí uvolňuje další řady toků, což do značné míry obnovuje počáteční množství linek absolutního toku.
OBRATY A AKTUÁLNÍ POMĚRY
Množství toků vytvářených v jádru trafo je úměrné magnetizační síle
(V OBLASTECH AMPERE) primárního a sekundárního vinutí.
Ampér-otáčka (I x N) je indikátorem magneticko-hnací síly, kterou lze chápat jako magnetomotorickou sílu produkovanou jedním ampérem proudu běžícího v cívce o 1 otáčce.
Tok, který je k dispozici v jádru transformátoru, obklopuje společně primární a sekundární vinutí.
Vzhledem k tomu, že tok je pro každé vinutí stejný, měly by být ampérové otáčky v každém, primárním a sekundárním vinutí vždy stejné.
Kvůli tomu důvodu:
IpNp = IsNs
Kde:
IpNp = ampér / otáčky v primárním vinutí
IsNs - ampér / otáčky v sekundárním vinutí
Vydělením obou stran výrazu
Ip , dostaneme:
Np / Ns = Is / Ip
od té doby: Es / Ep = Ns / Np
Pak: Ep / Es = Np / Ns
Taky: Ep / Es = Is / Ip
kde
- Ep = napětí aplikované na primární část ve voltech
- Es = napětí na sekundárním obvodu ve voltech
- Ip = proud v primárním v Amp
- Is = aktuální sekundární v ampérech
Všimněte si, že rovnice označují poměr ampérů jako inverzní poměr vinutí nebo poměr otáček, stejně jako poměr napětí.
To znamená, že transformátor, který má menší počet závitů na sekundární straně ve srovnání s primární, může snížit napětí, ale zvýšil by proud. Například:
Předpokládejme, že transformátor má poměr napětí 6: 1.
Pokuste se najít proud nebo zesilovače na sekundární straně, pokud je proud nebo zesilovač na primární straně 200 miliampérů.
Předpokládat
Ep = 6 V (jako příklad)
Is = 1V
Ip = 200 mA nebo 0,2 A
Je =?
Odpovědět:
Ep / Es = Is / Ip
Transpozice pro je:
Is = EpIp / Es
Střídání:
Is = (6V x 0,2A) / 1V
Je = 1,2 A.
Výše uvedený scénář řeší, že navzdory skutečnosti, že napětí na sekundárním vinutí je šestinová oproti napětí na primárním vinutí, zesilovače v sekundárním vinutí jsou 6krát vyšší než zesilovače v primárním vinutí.
Na výše uvedené rovnice lze velmi dobře pohlížet z alternativního hlediska.
Poměr vinutí znamená součet, kterým transformátor zvyšuje nebo zvyšuje nebo snižuje napětí připojené k primární straně.
Pro ilustraci předpokládejme, že pokud má sekundární vinutí transformátoru dvojnásobný počet závitů než primární vinutí, bude napětí stimulované na sekundární stranu pravděpodobně dvojnásobné než napětí na primárním vinutí.
V případě, že sekundární vinutí nese poloviční počet závitů na primární straně, bude napětí na sekundární straně poloviční než napětí na primárním vinutí.
To znamená, že poměr vinutí spolu s poměrem zesilovače transformátoru tvoří inverzní asociaci.
Výsledkem je, že zesilovací transformátor 1: 2 může mít polovinu zesilovače na sekundární straně ve srovnání s primární stranou. Transformátor sestupný 2: 1 může mít v sekundárním vinutí dvakrát vyšší zesilovač než primární strana.
Ilustrace: Transformátor s poměrem vinutí 1:12 má na sekundární straně proud 3 ampéry. Zjistit velikost zesilovačů v primárním vinutí?
Dané:
Np = 1 tah (například)
Ns = 12 otáček
Is = 3Amp
Lp =?
Odpovědět:
Np / Ns = Is / Ip
Střídání:
Ip = (12 otáček x 3 Amp) / 1 otáčka
Ip = 36A
Výpočet vzájemné indukčnosti
Vzájemná indukce je proces, při kterém jedno vinutí prochází indukcí EMF v důsledku rychlosti změny proudu sousedního vinutí vedoucí k indukční vazbě mezi vinutím.
Jinými slovy Vzájemná indukčnost je poměr indukovaného emf napříč jedním vinutím k rychlosti změny proudu na druhém vinutí, vyjádřený v následujícím vzorci:
M = emf / di (t) / dt
Fázování transformátorů:
Normálně, když zkoumáme transformátory, většina z nás věří, že napětí a proudy primárního a sekundárního vinutí jsou navzájem ve fázi. To však nemusí být vždy pravda. V transformátorech závisí vztah mezi napětím, fázovým úhlem proudu napříč primárním a sekundárním způsobem na tom, jak jsou tato vinutí otočena kolem jádra. Záleží na tom, zda jsou oba proti směru hodinových ručiček, nebo ve směru hodinových ručiček, nebo může být jedno vinutí otočené ve směru hodinových ručiček, zatímco druhé vinutí proti směru hodinových ručiček.
Pojďme se podívat na následující diagramy, abychom pochopili, jak orientace vinutí ovlivňuje fázový úhel:

Ve výše uvedeném příkladu vypadají směry vinutí identicky, to znamená, že primární i sekundární vinutí jsou otočeny ve směru hodinových ručiček. Díky této identické orientaci je fázový úhel výstupního proudu a napětí totožný s fázovým úhlem vstupního proudu a napětí.

Ve druhém příkladu výše je směr vinutí transformátoru vidět navinutý s opačnou orientací. Jak je vidět, primární se zdá být ve směru hodinových ručiček, zatímco sekundární je navinut proti směru hodinových ručiček. Kvůli této opačné orientaci vinutí je fázový úhel mezi dvěma vinutími o 180 stupňů od sebe a indukovaný sekundární výstup vykazuje odezvu fázového proudu a napětí.
Dotová notace a Dot úmluva
Aby nedocházelo k nejasnostem, používá se notace nebo konvence tečky, které představují orientaci vinutí transformátoru. To umožňuje uživateli porozumět specifikacím vstupního a výstupního fázového úhlu, ať už je primární a sekundární vinutí ve fázi nebo mimo fázi.
Konvence teček je implementována tečkovými značkami napříč počátečním bodem vinutí, což naznačuje, zda je vinutí navzájem ve fázi nebo mimo fázi.
Následující schéma transformátoru nese označení konvence tečky a znamená, že primární a sekundární transformátor jsou ve fázi navzájem.

Bodová notace použitá na ilustraci níže ukazuje DOT umístěné přes protilehlé body primárního a sekundárního vinutí. To naznačuje, že orientace vinutí obou stran není stejná, a proto bude fázový úhel napříč dvěma vinutími 180 stupňů mimo fázi, když se na jedno z vinutí použije AC vstup.

Ztráty ve skutečném transformátoru
Výpočty a vzorce uvažované v předchozích odstavcích byly založeny na ideálním transformátoru. V reálném světě a pro skutečný transformátor však může být scénář hodně odlišný.
Zjistíte, že v ideálním provedení budou ignorovány následující základní lineární faktory reálných transformátorů:
(a) Mnoho typů ztrát jádra, společně označovaných jako ztráty magnetizujícím proudem, které mohou zahrnovat následující typy ztrát:
- Ztráty hystereze: je to způsobeno nelineárními vlivy magnetického toku na jádro transformátoru.
- Ztráty vířivými proudy: Tato ztráta je generována v důsledku jevu zvaného joule zahřívání v jádře transformátoru. Je úměrná druhé mocnině napětí přivedeného na primární část transformátoru.
(b) Na rozdíl od ideálního transformátoru nemůže mít odpor vinutí ve skutečném transformátoru nikdy nulový odpor. Znamená to, že vinutí bude nakonec mít určitý odpor a indukčnosti spojené s nimi.
- Ztráty Joule: Jak bylo vysvětleno výše, odpor generovaný na svorkách vinutí vede ke ztrátám Joule.
- Únikový tok: Víme, že transformátory do značné míry závisí na magnetické indukci přes jejich vinutí. Protože jsou však vinutí postavena na společném jediném jádru, magnetický tok vykazuje tendenci k úniku přes vinutí přes jádro. To vede k impedanci zvané primární / sekundární reaktivní impedance, která přispívá ke ztrátám transformátoru.
(c) Protože transformátor je také druh induktoru, je také ovlivněn jevem, jako je parazitní kapacita a vlastní rezonance, z důvodu distribuce elektrického pole. Tato parazitní kapacita může obvykle být ve 3 různých formách, jak je uvedeno níže:
- Kapacita generovaná mezi tahy nad sebou uvnitř jedné vrstvy
- Kapacita generovaná ve dvou nebo více sousedních vrstvách
- Kapacita vytvořená mezi jádrem transformátoru a navíjecí vrstvou (vrstvami) ležící vedle jádra
Závěr
Z výše uvedené diskuse můžeme pochopit, že v praktických aplikacích nemusí být výpočet transformátoru, zejména transformátoru se železným jádrem, tak jednoduchý, jako by byl ideální transformátor.
Abychom získali co nejpřesnější výsledky pro data vinutí, možná budeme muset vzít v úvahu mnoho faktorů, jako jsou: hustota toku, plocha jádra, velikost jádra, šířka pera, plocha okna, typ materiálu jádra atd.
O všech těchto výpočtech se můžete dozvědět více pod tímto příspěvkem:
Předchozí: Ultrazvukový obvod indikátoru hladiny paliva Další: Srovnávací obvody využívající IC 741, IC 311, IC 339